안녕하세요, 산격동 너구리입니다.
이번 포스팅은,
SPSS를 이용한 "크루스칼 왈리스 검정"입니다.
개요
크루스칼 왈리스 검정이란??
분산 분석(ANOVA)에서 정규성 가정이 만족되지 않을 때 사용하는 비모수 검정법
ANOVA와는 달리 중앙값에 관한 결과를 얻을 수 있음.
가정
1. 표본은 독립적이다.
2. 측정값은 최소 순서형 변수이다. (대소 비교가 가능해야 합니다.)
비모수 검정은 가정에 있어서 상당히 자유롭지만,
일반적으로 비모수 검정이 검정력에서 더 좋지 않은 경향을 가집니다.
따라서, 모수 검정의 가정을 충족시키지 못할 때 사용하는 것이 비모수 검정이라고 보시면 되겠습니다.
가설
$H_0$ : 모든 그룹의 중앙값은 서로 같다.
$H_1$ : 모든 그룹의 중앙값이 전부 같은 것은 아니다.
예제
이전에 사용했었던 ANOVA 예제와 같은 파일로 하겠습니다.
A, B, C 고등학교 학생들의 하루 공부 시간을 조사했을 때,
고등학교 간에 공부 시간이 차이가 있는지 확인해보겠습니다.
위의 파일을 이용하였고, 통계적 유의수준은 0.05로 두었습니다.
데이터 불러오기


가정
ANOVA 가정을 만족시켰던 예시이므로,
당연하게 Kruskal Wallis test의 가정도 만족시키게 됩니다.
가설
$H_0$ : 세 고등학교 학생들의 평균 학습 시간은 전부 같다.
$H_1$ : 세 고등학교 학생들의 평균 학습 시간은 전부 같은 것은 아니다.
예제를 위해 임의로 지정한 가설입니다.
상황에 맞추어 적절히 변형하시길 바랍니다.
크루스칼 왈리스 검정
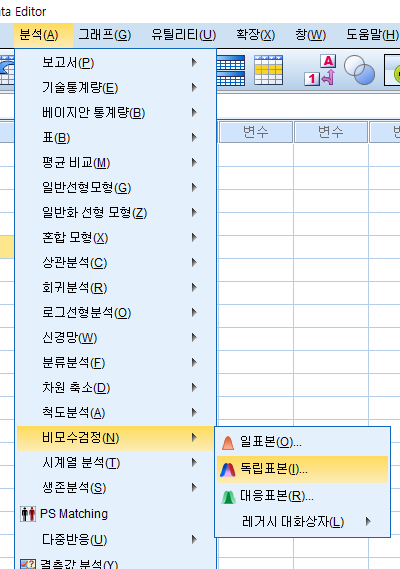

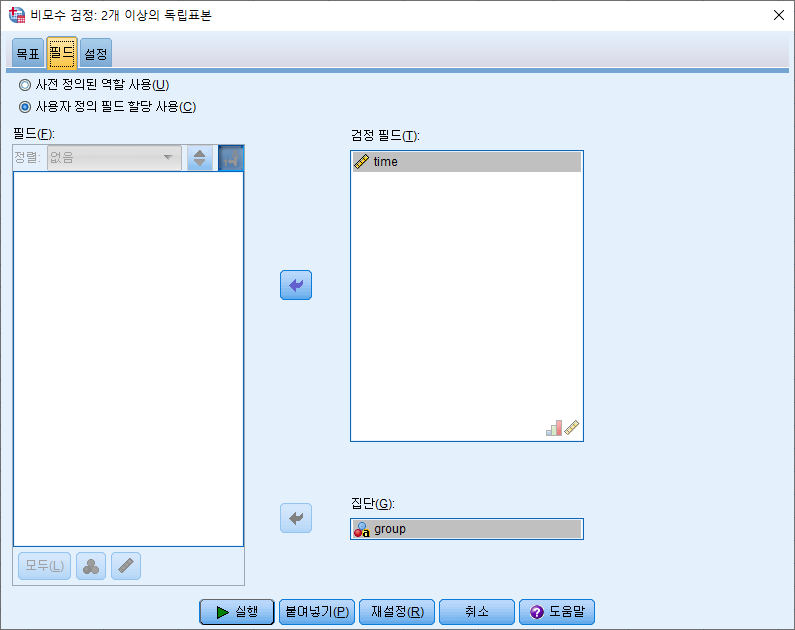

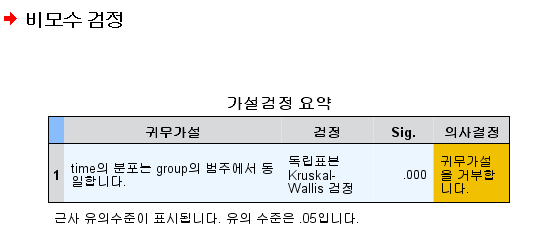
비모수 검정 결과 부분을 더블클릭해주시면 세부적인 정보를 보실 수 있습니다!!
사후 검정에 해당하는 대응별 비교의 결과를 보시려면 더블클릭을 해주셔야합니다~

"group"변수에 대한 p-value가 0.05 미만이므로 귀무가설을 기각합니다.
따라서, "세 고등학교 학생들의 공부시간 중앙값은 유의한 차이가 있다"라는 결론을 낼 수 있습니다.
사후 분석


아래에 보시면 [대응별 비교]탭이 있습니다.
해당 탭을 클릭해보면 위와 같은 결과를 확인하실 수 있습니다.
따라서,
"C 고등학교 학생들의 공부시간이 A, B 고등학교 학생들의 공부시간보다 유의하게 높음"을 알 수 있으며,
"A, B 고등학교 학생들의 공부 시간은 유의한 차이가 없음"을 확인할 수 있습니다.
이것으로 SPSS를 이용한 크루스칼 왈리스 검정에 대해 마치도록 하겠습니다.
이상, 산격동 너구리였습니다.
감사합니다.
* 잘못된 정보 및 오타가 포함되어 있을 수 있습니다.
그대로 받아들이시기보다는 다른 사람의 의견도 참고하셔서 분석하시길 바랍니다.
* 포스팅 내용 및 통계 분석 관련 질문은 언제나 환영입니다.
가능한 선에서 최대한 답변하도록 하겠습니다.
'내가 하는 통계 분석 > SPSS' 카테고리의 다른 글
| [내가 하는 통계 분석] Welch's ANOVA in SPSS (0) | 2021.02.16 |
|---|---|
| [내가 하는 통계 분석] Welch's T 검정(Welch's t-test) in SPSS (0) | 2021.02.16 |
| [내가 하는 통계 분석] 분산 분석(ANOVA, Analysis of Variance) in SPSS (0) | 2021.02.16 |
| [내가 하는 통계 분석] 윌콕슨 부호 순위 검정(Wilcoxon signed rank test) in SPSS (2) | 2021.02.16 |
| [내가 하는 통계 분석] 윌콕슨 순위합 검정(Wilcoxon rank sum test) or 맨-휘트니 U 검정(Mann-Whitney U test) in SPSS (7) | 2021.02.16 |