안녕하세요, 산격동 너구리입니다.
이번에도 이전 포스팅에 이어서 진행합니다.
[내가 하는 통계 분석] 회귀분석(2). 변수 선택법, 로그 변환 in R
안녕하세요, 산격동 너구리입니다. 저번에 이어 이번 포스팅도 "회귀분석"입니다. lunch-box.tistory.com/114 [내가 하는 통계 분석] 회귀분석(Regression) in R 안녕하세요, 산격동 너구리입니다. 이번 포스
lunch-box.tistory.com
이번에는 독립 변수의 고차항과 상호작용항을 추가해서 모형의 성능을 올려볼겁니다.
개요
고차항이란??
말그대로 차수가 높은 항입니다.
어떤 독립변수 $X$가 있다면, $X^k$인 독립변수를 추가하는 것입니다.
상호작용항이란??
영어로는 interaction term이라고 하고, 시너지라고 부르기도 합니다.
의미는 떠오르시는 것 그대로입니다.
어떤 일을 할 때도,
A를 할 때 힘든 정도와 B를 할 때의 힘든 정도가 있다고 하면
A와 B를 함께 할 때에는 단순히 더한 만큼 힘든 것보다 더 힘들 수 있습니다...
이런 효과를 보통 시너지 효과라고 이야기하는데,
상호작용항은 이러한 효과의 영향을 찾기 위해 추가됩니다.
보통 상호작용항은 각각의 독립 변수를 곱한 형태로 나타납니다.
예제
저번 포스팅에서 이어서 진행합니다.
따라해보실 분은 이전 포스팅 참고바랍니다.
이전 포스팅을 확인해보면,
youtube와 sales 간 산점도에서 약간 커브형태를 보여주었고,
잔차 그래프에서도 약간의 커브형태가 있었습니다.
따라서 2차항을 추가하면 좀 더 좋은 결과가 나올 것으로 생각됩니다.
2차항과 상호작용까지 추가하고, 단계적 선택법으로 변수를 선별하겠습니다.
2차항, 상호작용항 추가
## 2차항 + 상호작용항
model3 = lm(sales ~ .^2 +
I(youtube^2) +
I(facebook^2) +
I(newspaper^2)
, data = data)
summary(model3)
변수가 총 9개로 증가했습니다.
기존 3개 + 각각의 제곱 3개 + 서로 간 곱셈 3개 = 9개
설명력을 의미하는 $R^2$는 0.9865, 수정된 $R^2$는 0.9859입니다.
확실히 변수가 추가되니 성능이 올라간 것으로 보입니다.
그럼 이제 가정에 대해 확인해보겠습니다.
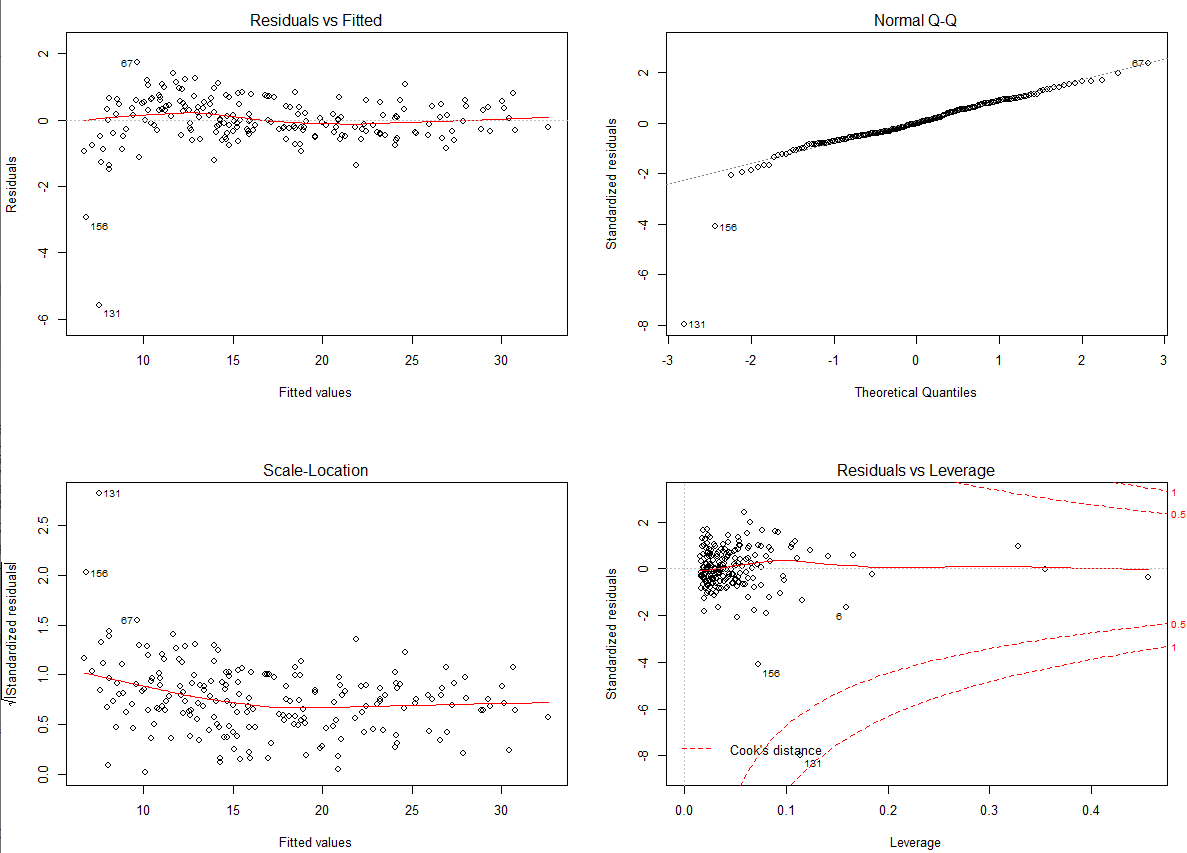
131번 관측치와 156번 관측치를 제외하면, 가정에서 큰 문제가 없어보입니다.
일단 2차항과 상호작용을 넣은 것은 모형에서 좋은 영향을 준 것으로 보입니다.
변수 선택
model3_selection = step(model3, direction = 'both',
scope = list(lower = ~1))
summary(model3_selection)
변수가 3개 제외되어 총 6개의 변수가 선택되었습니다.
설명력을 의미하는 $R^2$는 거의 차이가 없습니다.
잔차 그래프를 확인해보겠습니다.
plot(model3_selection)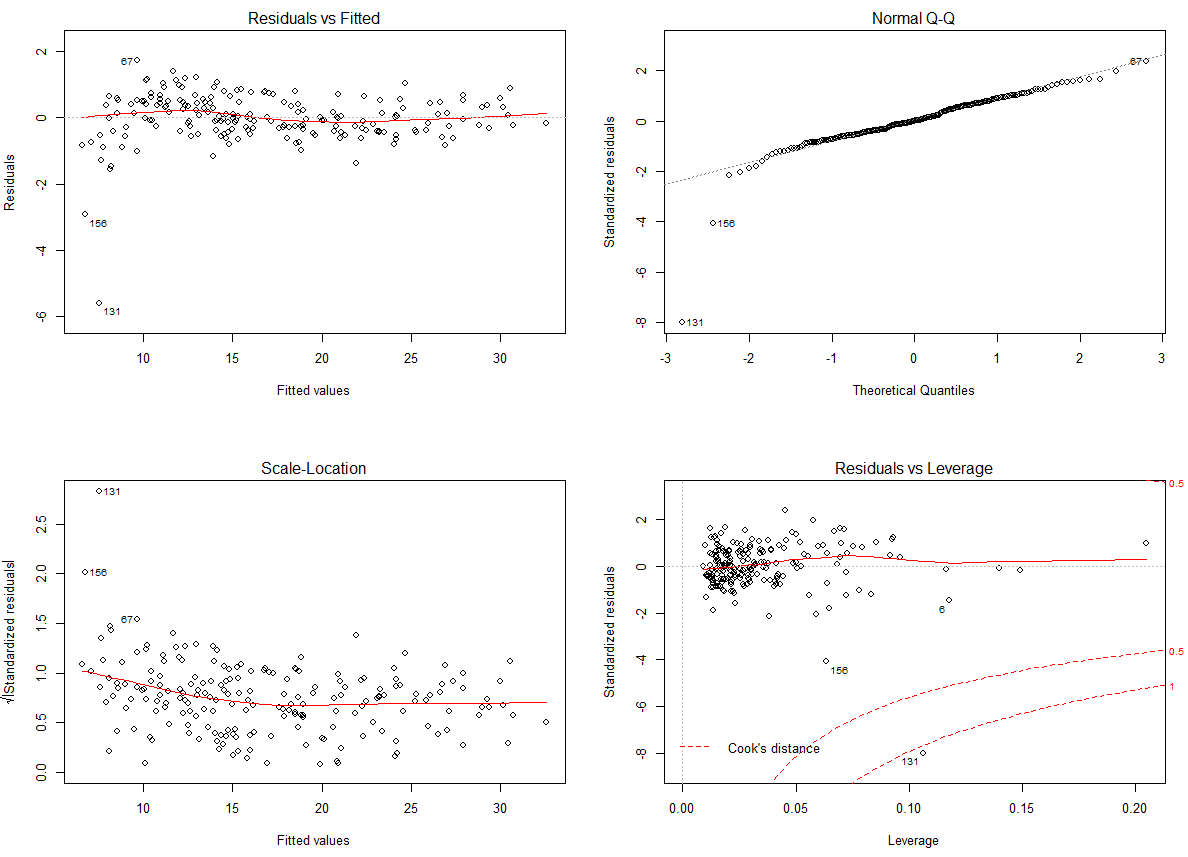
잔차 그래프는 거의 비슷한 것으로 보입니다.
131번, 156번 관측치만 아니라면 가정에서 큰 문제가 없을 것 같습니다.
그렇다고 해서, 131번과 156번 관측치를 제거하는 것은 바람직하지 않습니다.
하지만, 입력 오류가 있을 수도 있으니 확인해보는 것은 좋습니다.
입력 오류가 없다면, 왜 이 관측치들이 이상치를 가지는지 고민해보시길 바랍니다.
그런 고민을 통해 문제를 해결할 새로운 아이디어를 얻을 수 있습니다.
최종 모형 선택
현재 데이터는 광고와 매출에 관련된 데이터로 굉장히 복잡한 배경이 깔려있습니다.
복잡한 배경을 3개의 변수로 충분히 설명하기엔 무리가 있어보입니다.
그렇기 때문에, 지금 131번과 156번 관측치가 이상치로 나오는 것이 그리 이상한 것은 아닙니다.
예를 들어, 어떤 사업을 하느냐에 따라 광고와 매출의 관계가 달라질 수도 있겠죠.
이처럼 좀 더 의미있는 변수가 많다면, 가정을 만족시키면서 모형의 성능을 더 올릴 수도 있습니다.
물론 새로운 변수 없이도, 변수 변환을 통해 새로운 변수를 더 추가하고,
모형을 더 복잡하게 만들어서 성능을 조금 더 올릴 수 있을지도 모릅니다.
하지만, 그렇게해서 성능을 올린다하더라도 단점이 있습니다.
1) 변수 변환을 많이 할수록 해석이 어려움
2) 모형이 복잡해질수록 과적합의 문제가 있음
3) 귀찮음
그렇기 때문에 가능하면 적은 변수로 최대의 성능을 낼 수 있도록 해야합니다.
이때까지의 과정을 통해 newspaper 변수가 그다지 쓸모 없다는 생각이 들었습니다.
따라서, 위의 모형에서 newspaper 변수를 없앤 모형을 확인해보겠습니다.
## 최종
model4 = lm(sales ~ I(youtube^2) +
youtube + facebook + youtube*facebook
, data = data)
plot(model4)
잔차 그래프는 큰 차이가 없는 것 같습니다.
summary(model4)
$R^2$도 거의 차이가 없어보입니다.
독립 변수는 4개로 줄었지만, 성능에 있어서는 큰 차이가 없습니다.
모형의 가정이 완벽하진 않지만, 저는 이 모형을 최종 모형으로 선택하지 않을까 싶습니다.
통계학에서 "Simple is Best"라는 이야기가 있습니다.
일반적으로, 성능이 비슷하다면 변수의 수를 줄이는게 좋습니다.
목적에 따라 성능과 해석 사이에서 절충안을 잘 찾아내시길 바랍니다.
이것으로 3차례에 걸친 포스팅을 마무리하도록 하겠습니다.
이상, 산격동 너구리였습니다.
감사합니다.
* 잘못된 정보 및 오타가 포함되어 있을 수 있습니다.
그대로 받아들이시기보다는 다른 사람의 의견도 참고하셔서 분석하시길 바랍니다.
* 포스팅 내용 및 통계 분석 관련 질문은 언제나 환영입니다.
가능한 선에서 최대한 답변하도록 하겠습니다.
'내가 하는 통계 분석 > R' 카테고리의 다른 글
| [내가 하는 통계 분석] Sobel Test in R (0) | 2021.04.18 |
|---|---|
| [내가 하는 통계 분석] 매개효과 분석(Meditation Analysis) in R (0) | 2021.04.13 |
| [내가 하는 통계 분석] 회귀분석(2). 변수 선택법, 로그 변환 in R (0) | 2021.04.05 |
| [내가 하는 통계 분석] 회귀분석(1). 회귀분석(Regression) in R (0) | 2021.04.03 |
| [내가 하는 통계 분석] 스피어만 상관 계수(Spearman correlation coefficient), 켄달 타우 계수(Kendall tau coefficient) in R (0) | 2021.03.13 |